How to Estimate Entropy Wrong

The approach
Experiments and oops
What’s going on here?
Experiments with the fix
Some extra stuff
- Limiting density of discrete points
- Related mistake

One common attempt to estimate entropy from samples is via discretisation and counting. However, it can easily go wrong.

The approach

This particular approach I refer to for entropy estimation consists three steps:

Discretise data into $N$ bins
Count data and normalise the counts into probabilities $\{p_i\}_{i=1}^{N}$
Estimate the entropy as $-\sum_i p_i \log p_i$

Intuitively, we may also believe with more data and a large $N$ , we can get a good estimate.

Experiments and oops

This method sounds reasonable and it’s worth to check how it performs on simulated Gaussian random variables, for which we know the ground truth entropy. For this I simulated $10,000$ samples from Gaussians with $0$ mean and standard deviation $\sigma \in [0.1, 1, 5, 10, 15, 20]$ . For binning, I uniformly discretise the data into $20$ bins. Figure 1 shows the estimated entropy as well as the ground truth, computed as $\log(\sigma \sqrt{2 \pi e})$ .

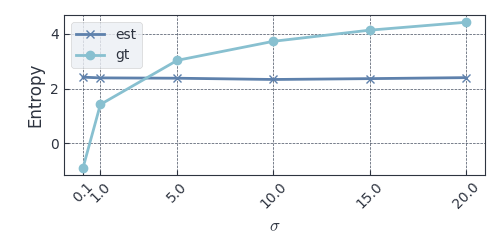
Figure 1: Estimated (est) and ground truth (gt) entropy for $10,000$ Gaussians with $\sigma$ varying

Looks not only the estimates differ from the ground truth a lot (except somewhere between $\sigma=1$ and $\sigma=5$ which is close) but also stays almost constant with varying $\sigma$ , which is a bit unexpected. Would it be because the number of bins we set is just too bad? To check this, I perform the same experiments but now with $\sigma = 1$ fixed and the number of bins varying $N \in [10, 20, 30, 40]$ ; figure 2 shows the results.

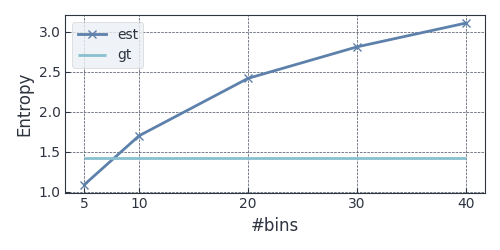
Figure 2: Estimated (est) and ground truth (gt) entropy for $10,000$ Gaussians with $N$ varying

So it looks like for this particular $\sigma$ , there is only one binning size $N$ that gives close estimate. This doesn’t help the situation and is away from our intuition of increasing $N$ may give a better estimate. To make sure this is not a special case for this particular $\sigma$ , I check the effect of $\sigma$ and $N$ in a single picture by varying both $\sigma$ and the number of bins, which given the contour plot in figure 4.

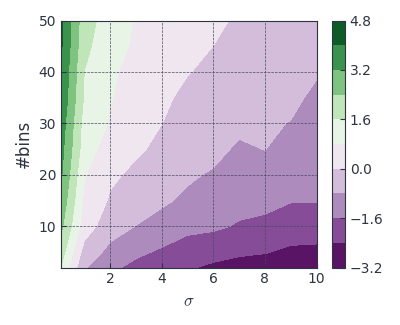
Figure 3: Difference between estimated (est) and ground truth (gt) entropy for $10,000$ Gaussians with $\sigma$ and the number of bins varying

Looks like there is some particular number of bins (see the boundary for difference equal to $0$ in colo bar) required for a different $\sigma$ unlike one might hope we can simply improve the estimate by using more bins. This almost makes this estimate useless because there is no easy way to tune it without knowing the ground truth.

What’s wrong and is there something we can do to have it fixed?

What’s going on here?

To understand what’s going on here, we need to review some basic concepts.

Entropy and differential entropy

The entropy (or discrete entropy or Shannon entropy) itself is only defined for discrete probability distributions. For a discrete distribution with support $\{x_1, \dots, x_C\}$ of the random variable $X$ , the entropy $H$ is defined as

$\begin{equation*} H(X) = -\sum_{c=1}^{N} p_c \log p_c \end{equation*}$

where $p_c := P(X = x_c)$ .

For continuous distributions, the correspondence is differential entropy, suggested by Claude Shannon without a formal justification¹¹ By this I mean, to extend the idea of entropy, Shannon simply made an analogue of the discrete entropy instead of deriving it, according to the Wikipedia page.. For a continuous distribution with probability density function $f$ and support $\mathcal{X}$ , the differential entropy is defined as

$\begin{equation*} h(X) = \int_{\mathcal{X}} f(x) \log(f(x)) \deriv x. \end{equation*}$

What entropy are we estimating?

The first thing to note here is that (by using “the approach” in the beginning) we are attempting to approximating the differential entropy (for the target continuous random variable) via entropy (for the discretised version). The first question to ask is: Is this idea/goal correct?

Approximating the differential entropy

Although intuitively one might think if we have an infinite number of data points and keep increasing the number of bins, we can approximate the target differential entropy pretty well, this is actually not true.

To see the connection between differential entropy and (discrete) entropy, we start with the following equivalence for any continuous function $f$ discretised into bins of size $\Delta$

$\begin{equation*} \int_{-\infty}^{\infty} f(x) \deriv x = \lim_{\Delta \to 0} \sum_{i=-\infty}^{\infty} \Delta f(x_i) \end{equation*}$ 1

where $\Delta f(x_i) = \int_{\Delta i}^{\Delta (i+1)} f(x) \deriv x$ , following the mean-value theorem²² No panic—the mean-value theorem basically says these $x_i$ exisit..

Then using the relationship between bin proportion $p_i$ , bin size $\Delta$ and density $f$ , $p_i = \Delta f(x_i)$ , we can write down the Shannon entropy of the discretised density $H_\Delta$

$\begin{equation*} H_\Delta := - \sum_{i=-\infty}^{\infty} p_i \log(p_i) = - \sum_{i=-\infty}^{\infty} \Delta f(x_i) \log(\Delta f(x_i)) = -\sum_{i=-\infty}^{\infty} \Delta f(x_i) \log(f(x_i)) - \sum_{i=-\infty}^{\infty} \Delta f(x_i) \log(\Delta), \end{equation*}$

where the second equality is simply based on the property of logorithm³³ That is $\log(a b) = \log(a) + \log(b)$ ..

Taking the limit $\Delta \to 0$ , using the property in equation 3 we have

$\begin{equation*} \lim_{\Delta \to 0} H_\Delta = \underbrace{-\int_{-\infty}^{\infty} f(x) \log(f(x)) \deriv x}_{\text{differential entropy}} \underbrace{-\log(0)}_{\text{infinty offset}}. \end{equation*}$

This is actually a known fact that the differential entropy is not a limit of the Shannon entropy and there is in fact an infinite offset/bias in the limit!⁴⁴ Besides, the differential entropy also lacks a number of properties that Shannon entropy has such as positivity or invariant to change of variables.

Importantly for us, this explain why we saw a monotonically increasing line in figure 2—we are simply pushing $-\log(\Delta)$ with a decreasing $\Delta$ !

The fix

The clear fix is to use the following equality we have established so far:

$\begin{equation*} \underbrace{-\int_{-\infty}^{\infty} f(x) \log(f(x)) \deriv x}_{h(X)} = -\lim_{\Delta \to 0} \sum_{i=-\infty}^{\infty} \Delta f(x_i) \log(f(x_i)) \end{equation*}$

together with the relation $p_i = \Delta f(x_i)$ , which gives:

$\begin{equation*} h(X) = -\lim_{\Delta \to 0} \sum_{i=-\infty}^{\infty} p_i \log(p_i / \Delta) \approx \underbrace{-\sum_{i=1}^{N} p_i \log(p_i / \Delta_i)}_{\text{our new estimator}} \end{equation*}$

where $\Delta_i$ is the bin size for bin $i$ .

In fact, what we just derived is referred as the histogram estimator of entropy in the literature.

Experiments with the fix

Let’s repeat the last experiment with this fix! The results is given in Figure 4.

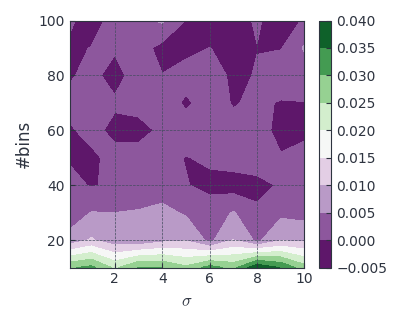
Figure 4: Difference between estimated (est) and ground truth (gt) entropy for $10,000$ Gaussians with $\sigma$ and the number of bins varying (fixed)

Great! Now with a reasonable large number of bins ( $>30$ ) our estimator work pretty nice! Below is the same experiment but did for Gamma and Beta with varying one of their parameters (I only do this because it’s a single input change to my script which uses Distributions.jl🙂):

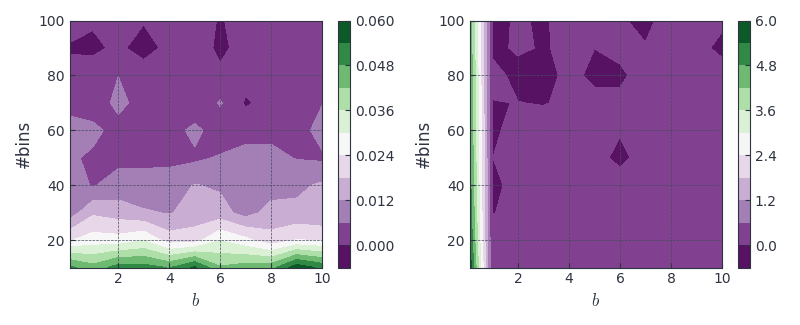
Figure 5: Difference between estimated (est) and ground truth (gt) entropy for $10,000$ Gamma( $2, b$ ) (left) and Beta( $2, b$ ) with $b$ and the number of bins varying (fixed)

Looks like the estimator still works pretty well except from some very skewed case like Beta( $2, 0.1$ ) (left most of the right plot).

🎉

Some extra stuff

Limiting density of discrete points

On the other side, the actual limit of the (Shannon) entropy is referred as the limiting density of discrete points (LDDP), suggested by [Jaynes, 1957], which is defined as

$\begin{equation*} \lim_{N\to\infty} H_N(X) = \log(N) - \int_\mathcal{X} f(x) \log({f(x) \over g(x)}) \deriv x, \end{equation*}$

where $g$ is the density of a uniform distribution over the support of $f$ . This actually looks interesting because it’s in fact the Kullback–Leibler divergence between $f$ and $g$ !

For a 1D case where the domain is $r$ , we simply have $g(x) = 1/r$ . With some moving-around and using $\log(N) = \int_\mathcal{X} f(x) \log(N) \deriv x$ ⁵⁵ Simply because $f$ is a probability density and it’s true for any density function $f$ and constant $C$ that $C = 1 C = \int f(x) \deriv x C = \int_\mathcal{X} f(x) C \deriv x$ ., we have

$\begin{equation*} \lim_{N\to\infty} H_N(X) = - \int_\mathcal{X} f(x) \log({f(x) r \over N}) \deriv x, \end{equation*}$

where $r / N$ is actually the bin size with uniform binning!

Importantly, this also reveals a fact to us: What we estimate is the entropy of truncated Gaussian where the truncation is done as the min and max of the samples—as we have no way to distinguish if it’s really truncated or not beyond this!

Related mistake

Another mistake could arise from estimating the mutual information based on the same strategy. Moreover the mutual information between discrete variables also has different properties than that of continuous variables—see their wiki pages for more information.

References

[Jaynes, 1957]

Jaynes, E. T. (1957). Information theory and statistical mechanics. Physical review, 106(4):620.

By this I mean, to extend the idea of entropy, Shannon simply made an analogue of the discrete entropy instead of deriving it, according to the Wikipedia page.

No panic—the mean-value theorem basically says these $x_i$ exisit.

That is $\log(a b) = \log(a) + \log(b)$ .

⁴

Besides, the differential entropy also lacks a number of properties that Shannon entropy has such as positivity or invariant to change of variables.

⁵

Simply because $f$ is a probability density and it’s true for any density function $f$ and constant $C$ that $C = 1 C = \int f(x) \deriv x C = \int_\mathcal{X} f(x) C \deriv x$ .